算法设计与分析学习笔记

一、课程主要内容

二、本节课的主要内容

三、算法设计的要点

四、本节课涉及的问题

• 货郎问题

• 0-1背包问题

• 双机调度问题

• NP-hard问题

• .......

五、货郎问题

注：课后作业要用到。

六：算法的两种时间复杂度

最坏时间复杂度和平均时间复杂度。

七、算法的伪代码描述

八、函数的渐近的界

• 大O符号（描述一个函数的“上界”）

• Ω符号（描述一个函数的“下界”）

• 小o符号（描述一个更“严格”的上界）

• 小w符号（描述一个更“严格”的下界）

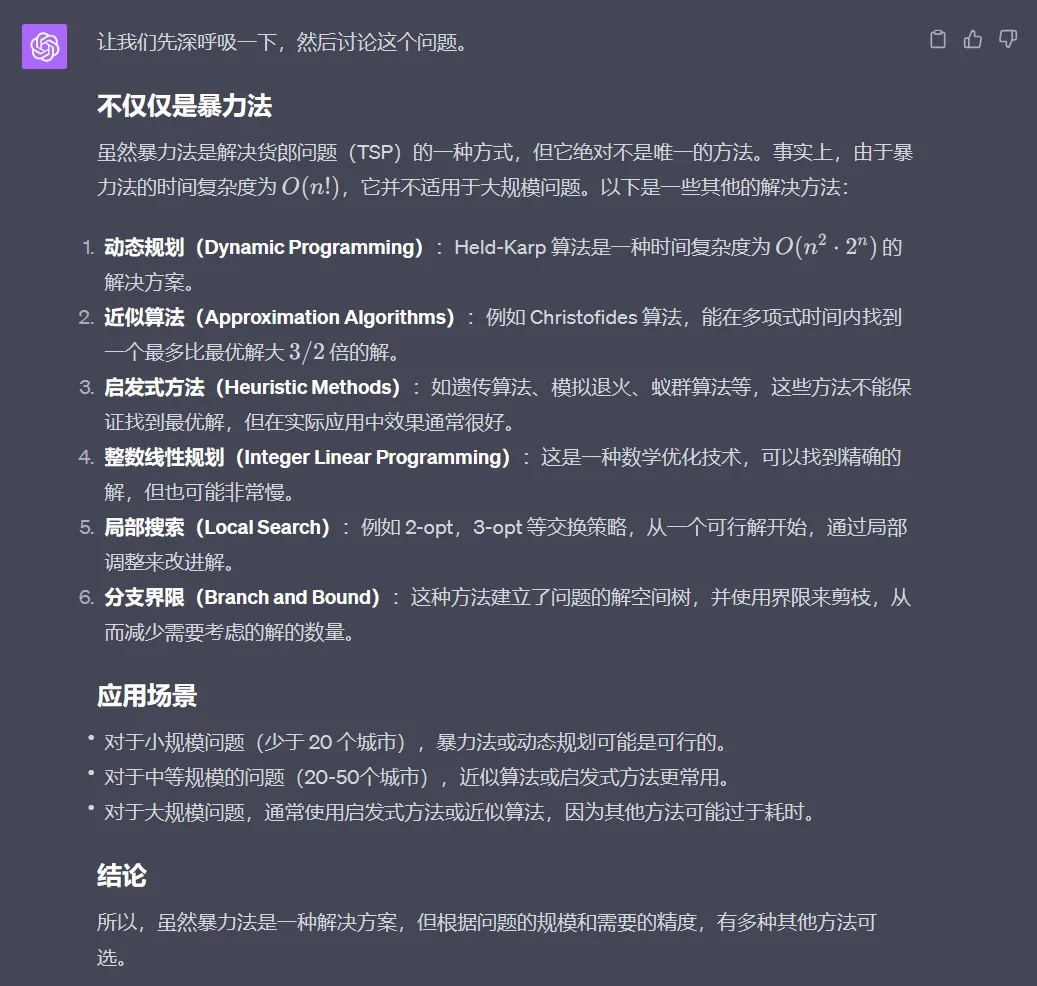
课后作业

用python或java简单实现货郎问题(TSP,Traveling Salesman Problem)。

from itertools import permutations  # 导入排列函数

# 定义城市和它们之间的距离
cities = ["c1", "c2", "c3", "c4"]
distances = {
    ("c1", "c2"): 10,
    ("c1", "c3"): 5,
    ("c1", "c4"): 9,
    ("c2", "c3"): 6,
    ("c2", "c4"): 9,
    ("c3", "c4"): 3,
}


# 函数：计算给定路径的总距离
def calculate_distance(path, distances):
    total_distance = 0  # 初始化总距离为0
    for i in range(len(path) - 1):  # 遍历路径中的每一对相邻城市
        # 使用get方法从字典中提取城市对的距离，如果没有则尝试反向城市对
        total_distance += distances.get(
            (path[i], path[i + 1]), distances.get((path[i + 1], path[i]), 0)
        )
    return total_distance  # 返回总距离


# 生成所有可能的路径（排列）
all_paths = list(permutations(cities))

# print(all_paths)
# print(len(all_paths))

# 寻找具有最小距离的路径
min_distance = float("inf")  # 初始化最小距离为无穷大
min_path = None  # 初始化最短路径为None

# 遍历所有可能的路径
for path in all_paths:
    path_with_return = path + (path[0],)  # 在路径末尾添加起始城市，形成一个回路
    distance = calculate_distance(path_with_return, distances)  # 计算回路的总距离
    if distance < min_distance:  # 如果找到更短的路径，则更新最小距离和最短路径
        min_distance = distance
        min_path = path_with_return

# 输出最短路径和其总距离
print(min_path, min_distance)

九、补充

教材—算法设计与分析（第2版）