动态规划学习笔记

1、动态规划就是：给定一个问题，我们把它拆成一个个子问题，直到子问题可以直接解决。然后把子问题的答案保存起来，以减少重复计算。再根据子问题答案反推，得出原问题解的一种方法。

关键词

记忆化搜索（备忘录）

2、动态规划入门思路：dfs暴力—>记忆化搜索—>动态规划（递推）

3、递归的过程：“归”的过程才是产生答案的过程，“递”的过程是分解子问题的过程。

4、

“递"--> 自顶向下

“归”--> 自底向上

5、递归搜索树的底是已知最小子问题的答案。

6、

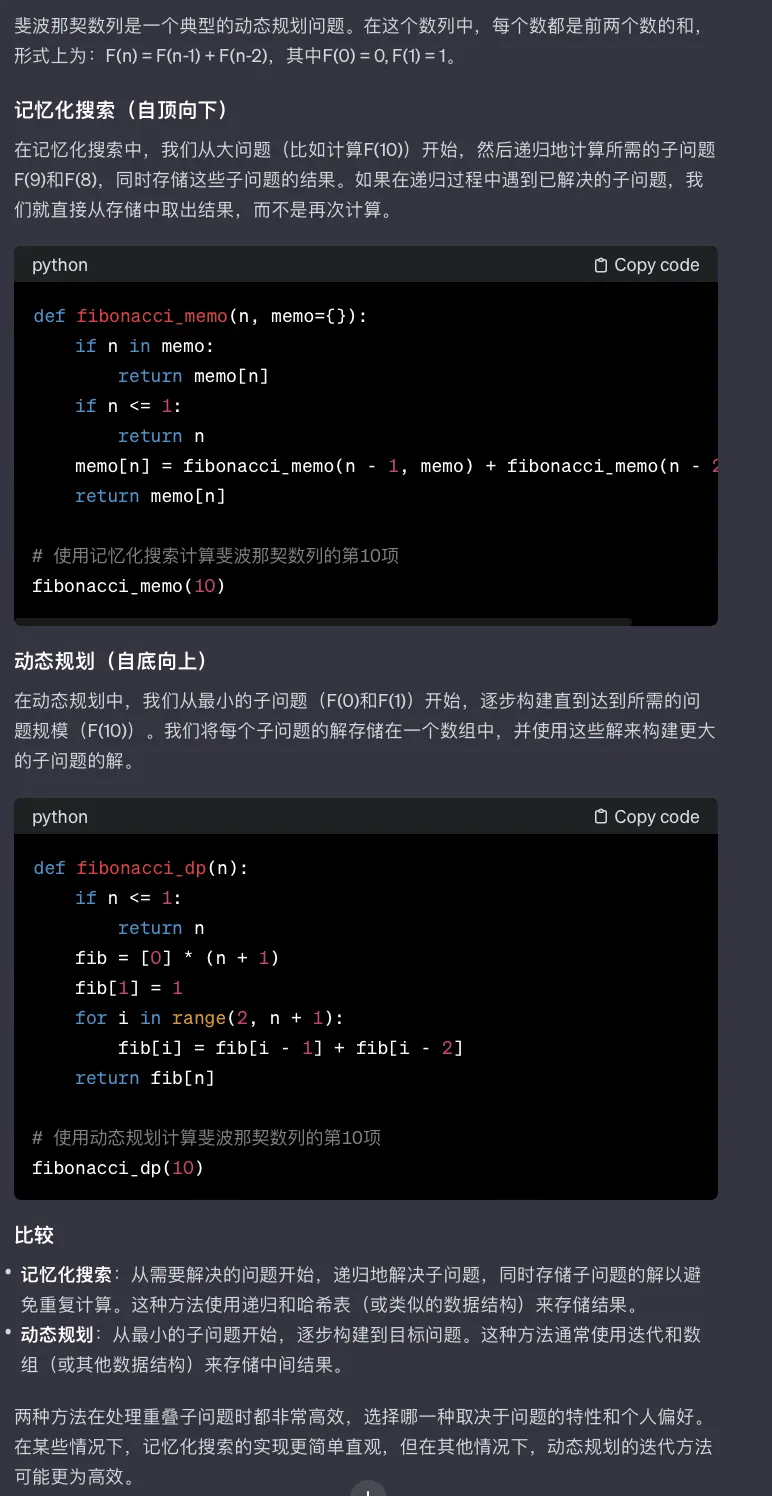
记忆化搜索 = 暴力dfs +记录答案

递推的公式= dfs 向下递归的公式

递推数组的初始值 = 递归的边界

7、动态规划，偏向全局最优，贪心法偏向局部最优。

8、以下关于动态规划法的描述哪些是正确的？

A.将问题分解成多级或许多子问题，然后顺序求解子问题。

B.可以确保得到最佳解

C.前一个子问题的解为后一个子问题的求解提供有用的信息。

D.从问题某一初始或推测值出发，一步步的攀登给定目标。

E.尽可能快的去逼近更好的解，当达到某一步不能继续时终止。

答案：A、C、D、E

链接：https://www.nowcoder.com/questionTerminal/ad0b237fcfe1468fb8fdb24b135586ae

9、动态规划入门习题

https://www.luogu.com.cn/paste/xac615na

10、动态规划的基本思想：

保存已解决的子问题结果，在需要时直接使用已求得的结果，避免大量重复计算，从而得到多项式时间算法。一记忆法

11、分治法 vs 动态规划法

相同：

原问题分解为子问题，求解子问题，得到原问题的解
前后存在递推关系

不同：

对分治算法，要求子问题独立；对动态规划，要求子问题重叠。

12、贪心、分治、动态规划

贪心：逐步构造解，以局部最优的贪婪准则构造。
分治：把原问题分为子问题，解决子问题，合并得到原问题的解。
动态规划：把原问题分为交叉的子问题。解决子问题，记录子问题的解，合并为原问题的解。

13、记忆化搜索（备忘录）vs 动态规划

例子：

14、动态规划基本要素

最优子结构性质：原问题的最优解包含子问题的最优解
重叠子问题性质：递归算法求解问题时，每次产生的子问题并不总是新问题，有些子问题被反复计算多次
无后效性：问题的全过程可以分为若干个阶段，而且在任何一个阶段x后的行为都只仅仅依赖于x的状态，而与x之前如何达到这种状态的方式无，这样的过程就构成了一个多阶段决策过程。未来与过去无关。

15、

贪心算法

最优子结构
无后效性
贪心选择

动态规划

最优子结构
无后效性
子问题重叠

16、动态规划算法的求解步骤

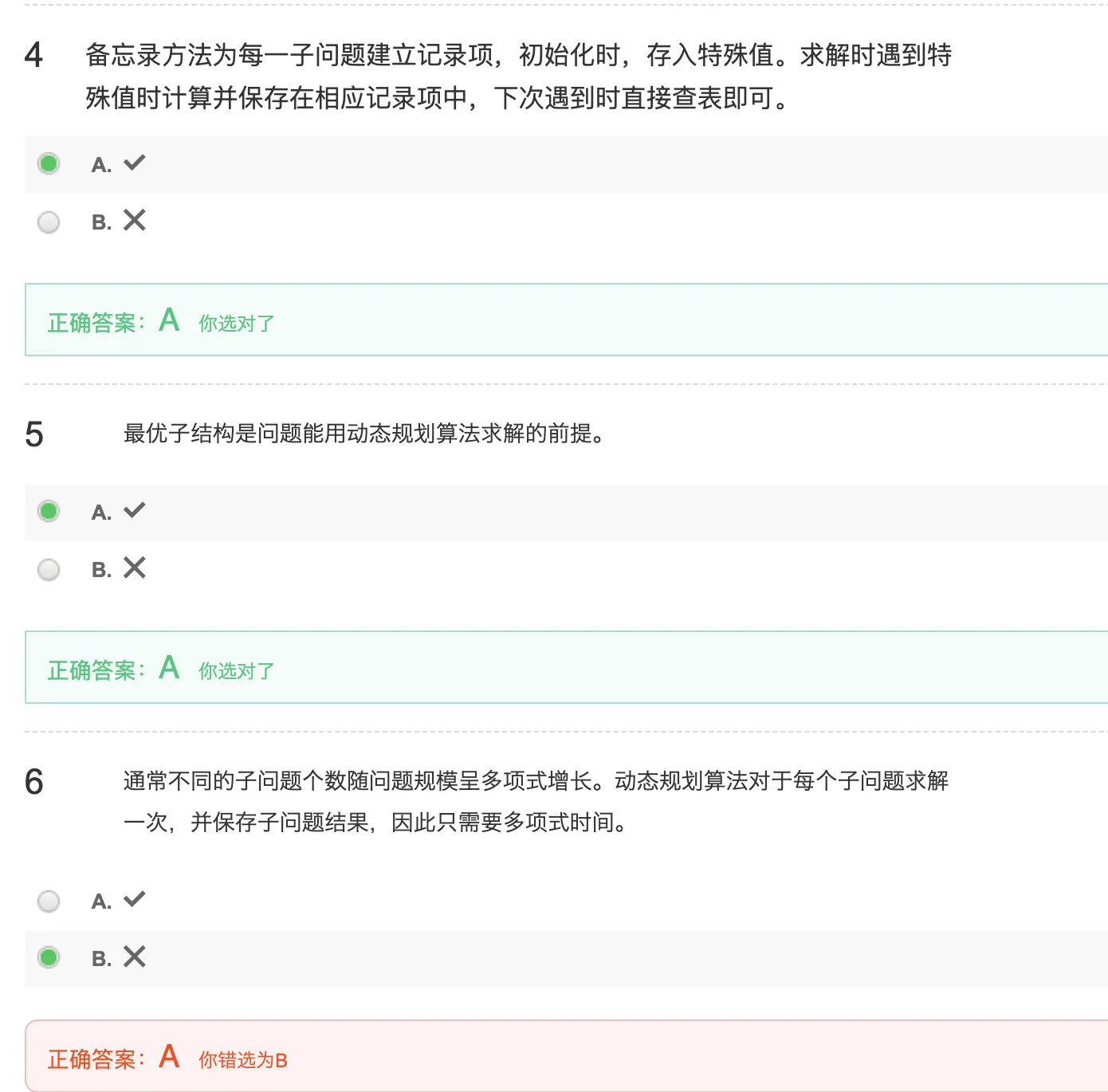
17、动态规划课后习题

18、0-1背包、恰好装满的0-1背包、完全0-1背包、多重0-1背包

0-1背包问题：选择物品放入固定容量的背包，以最大化价值，每个物品只能选或不选。
恰好装满的0-1背包问题：在0-1背包的基础上，要求背包被恰好装满。
完全0-1背包问题：每种物品可以选无限多个。
多重0-1背包问题：每种物品有数量限制。

19、动态规划策略通常用于求解最优化问题。在这类问题中，可能会有许多可行解。每一个解都对应于一个值，我们希望找到具有最优值的那个解，即最优解。

20、动态规划算法的基本步骤

a.分析最优解的结构

b.递归定义最优值

c.计算最优值

d.构造最优解