算法设计与分析学习笔记

网络流算法学习笔记

1、网络

2、最大流最小割定理

3、最大流FF(Ford-Fulkerson算法)

4、Edmonds-Karp 算法

Ford-Fulkerson 算法的特例。

5、Dinic算法

6、阻塞流

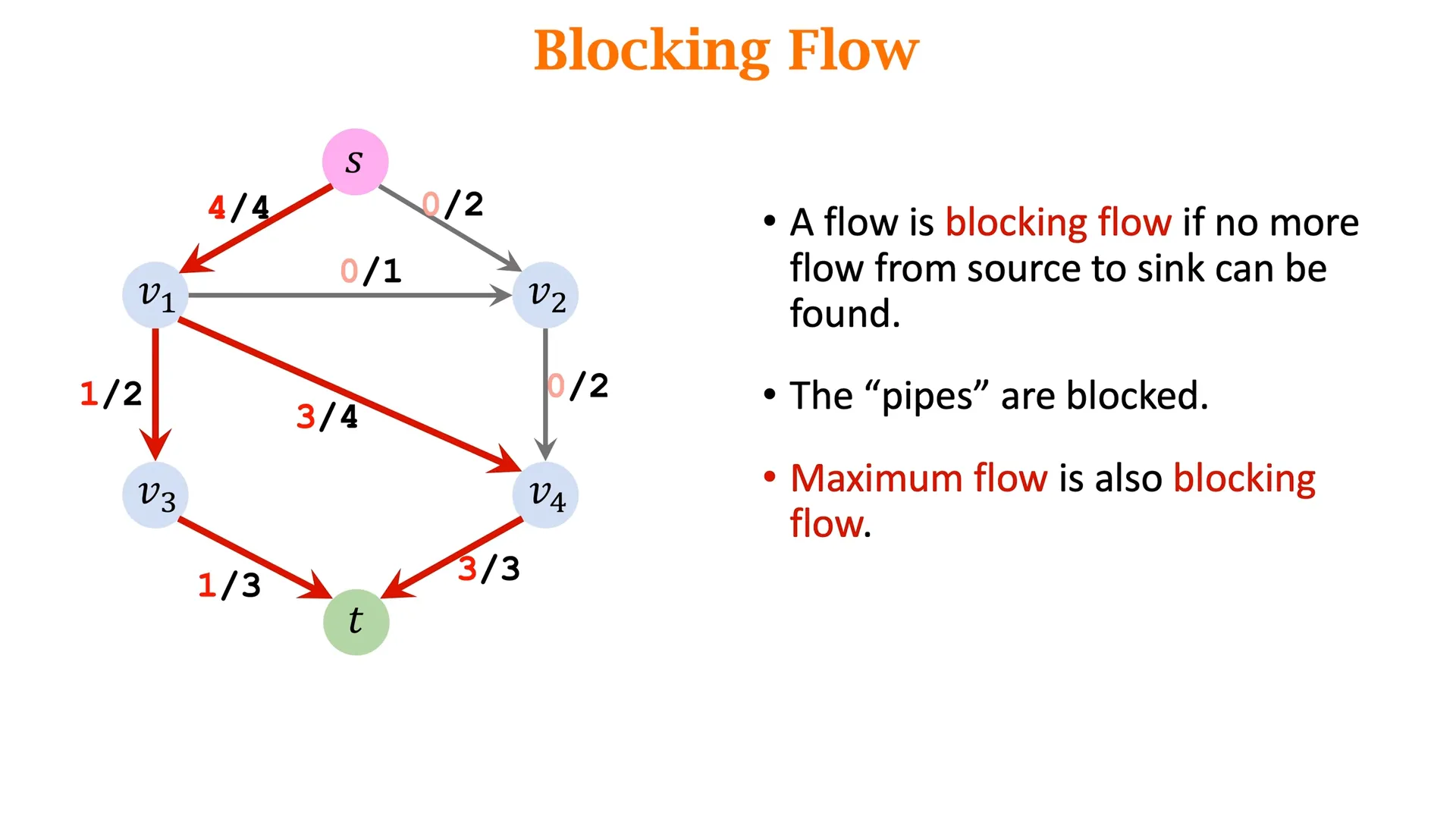
7、最大流和最小割的值相等。

8、最大流、最小割选择题

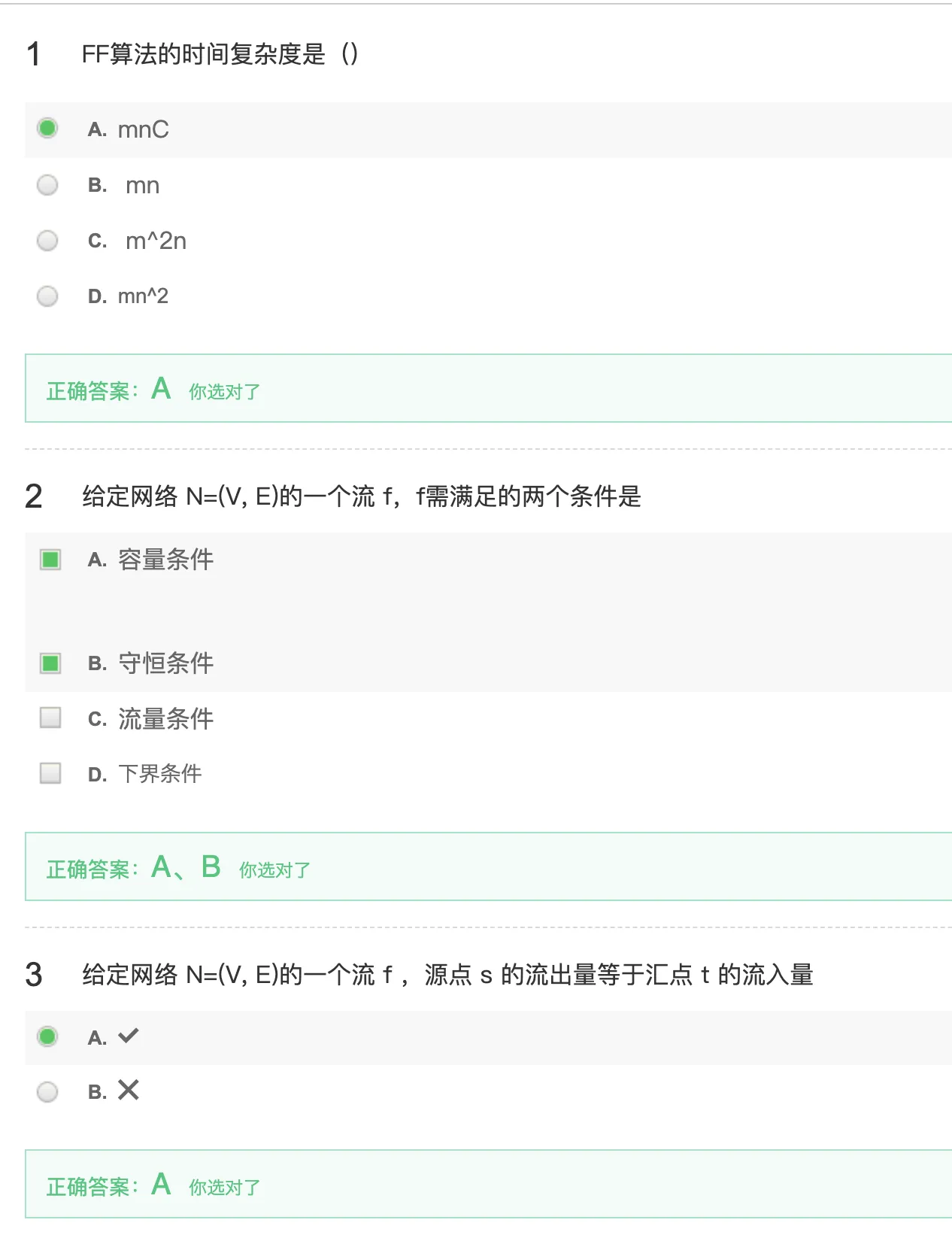
9、最大流算法选择题

10、割的容量计算的是流入边，不是流出边。

11、

1、在最大流问题中，哪种算法是用来寻找增广路径的？

A.深度优先搜索 (DFS)
B.广度优先搜索 (BFS)
C.贪心算法
D.动态规划
答案与解析: 选项 (2) 广度优先搜索 (BFS)。
例如，Ford-Fulkerson 方法中使用的 Edmonds-Karp 算法就是利用 BFS 来寻找增广路径。

2、在网络流中，如果一个网络的最大流为 k，则从源点到汇点的最小割的容量是多少？

A.小于 k
B.等于 k
C.大于 k
D.无法确定
答案与解析: 选项 (2) 等于 k。
根据最大流最小割定理，网络的最大流值等于从源点到汇点的最小割的容量。

3、在最大流问题中，每条边的流量必须满足哪两个条件？

A.不超过该边的容量且等于该边的容量
B.不超过该边的容量且为非负值
C.等于该边的容量且为非负值
D.为负值或等于该边的容量
答案与解析: 
选项 (2) 不超过该边的容量且为非负值。流量不能超过边的容量，并且必须是非负值。

填空题
1、在网络流问题中，________ 定义了网络中每个节点除源点和汇点外的流量平衡条件。

答案与解析: 
流量守恒 (Flow Conservation)。在每个中间节点，进入该节点的总流量必须等于离开该节点的总流量。

2、在 Ford-Fulkerson 算法中，如果在残余网络中不存在从源点到汇点的路径，则算法________。

答案与解析:
终止 (Terminates)。Ford-Fulkerson 算法在残余网络中寻找从源点到汇点的增广路径，
如果没有这样的路径存在，算法得出最大流并终止。