选择题
1、算法必须具备输入、输出和(D)等4个特性。
A. 可行性和安全性
B.确定性和易读性
C. 有穷性和安全性
D. 有穷性和确定性
答案:D
解析:
算法是解决问题的一系列明确的步骤。要成为有效的算法,它必须具备几个关键特性:
输入:算法应有零个或多个输入。
输出:至少有一个输出,即算法的结果。
有穷性:这意味着算法必须在执行有限的步骤后终止。这是非常关键的,
因为如果一个算法永远不会结束,那么它就不能用来有效地解决实际问题。
算法必须保证在经过一定数量的步骤后能够达到结束状态,无论是成功找到答案还是确定无解。
确定性:算法的每一步骤都必须明确无误,不能有歧义。这意味着在相同的输入下,
算法应该产生相同的输出。
2、算法分析中,记号O表示(),记号Ω表示(A)
A.渐近下界
B.渐近上界
C.非渐近上界
D.非渐近下界
答案:B,A
解析:
大O表示法 (Big O Notation) - 表示渐近上界
大O表示法用于描述算法性能的上限。它代表了算法在最坏情况下的运行时间复杂度。
例如, 如果一个算法的时间复杂度为O(n²), 这意味着在最坏情况下,算法的运行
时间是输入大小的平方的函数。
大Ω表示法 (Big Omega Notation) - 表示渐近下界
大Ω表示法用于描述算法性能的下限。它代表了算法在最佳情况下的运行时间复杂度。
例如, 如果一个算法的时间复杂度为Ω(n), 这意味着在最佳情况下,算法的运行时
间至少与输入大小成正比。
这两种表示法帮助我们从两个不同的角度理解算法的性能:
大O描述了算法可能的最慢速度,而大Ω描述了算法可能的最快速度。
题2拓展补充:
1、假设有两个函数 f(n) = n² 和 g(n) = n³,那么 g(n) 与 f(n) 的关系是什么?
答案:f(n) = O(g(n))
解析:

2、如果 h(n) = 3n + 2,j(n) = 5n,则 h(n) 和 j(n) 的关系是什么?
答案:h(n) = Θ(j(n))
解析
这两个函数的主导项都是线性的(即 n),所以它们的增长率相同。
因此,h(n) = Θ(j(n)),表示两者具有相同的渐近增长率。
3、对于函数 k(n) = n² + n 和 m(n) = 2n²,k(n) 是什么关系?
答案
k(n) = Θ(m(n))
解析
尽管 k(n) 包含一个 n² 和一个 n 项,但它的主导项是 n²,这与 m(n) = 2n² 的主导项相同。
因此,这两个函数在增长率上是相似的,即 k(n) 和 m(n) 是同阶的,k(n) = Θ(m(n))。
这意味着在大的输入值时,这两个函数的增长率相似。
补充资料

3、假设某算法在输入规模为 n 时的计算时间为 T(n) = 3*2^n。在某台计算机上实现并完成该算法的时间为 t 秒。现有另一台计算机,其运行速度为第一台的 64 倍,那么在这台新机器上用同一算法在 t 秒内能解输入规模多大的问题?
A. n+8
B. n+6
C. n+7
D. n+5
答案:B
解析:

4、设问题规模为 N 时,某递归算法的时间复杂度记为 T(N),已知 T(1) = 1,T(N) = 2T(N/2) + N/2,用 O 表示的时间复杂度为()。
A. O(logN)
B. O(N)
C. O(NlogN)
D. O(N^2logN)
答案:C
解析:涉及知识点—主定理
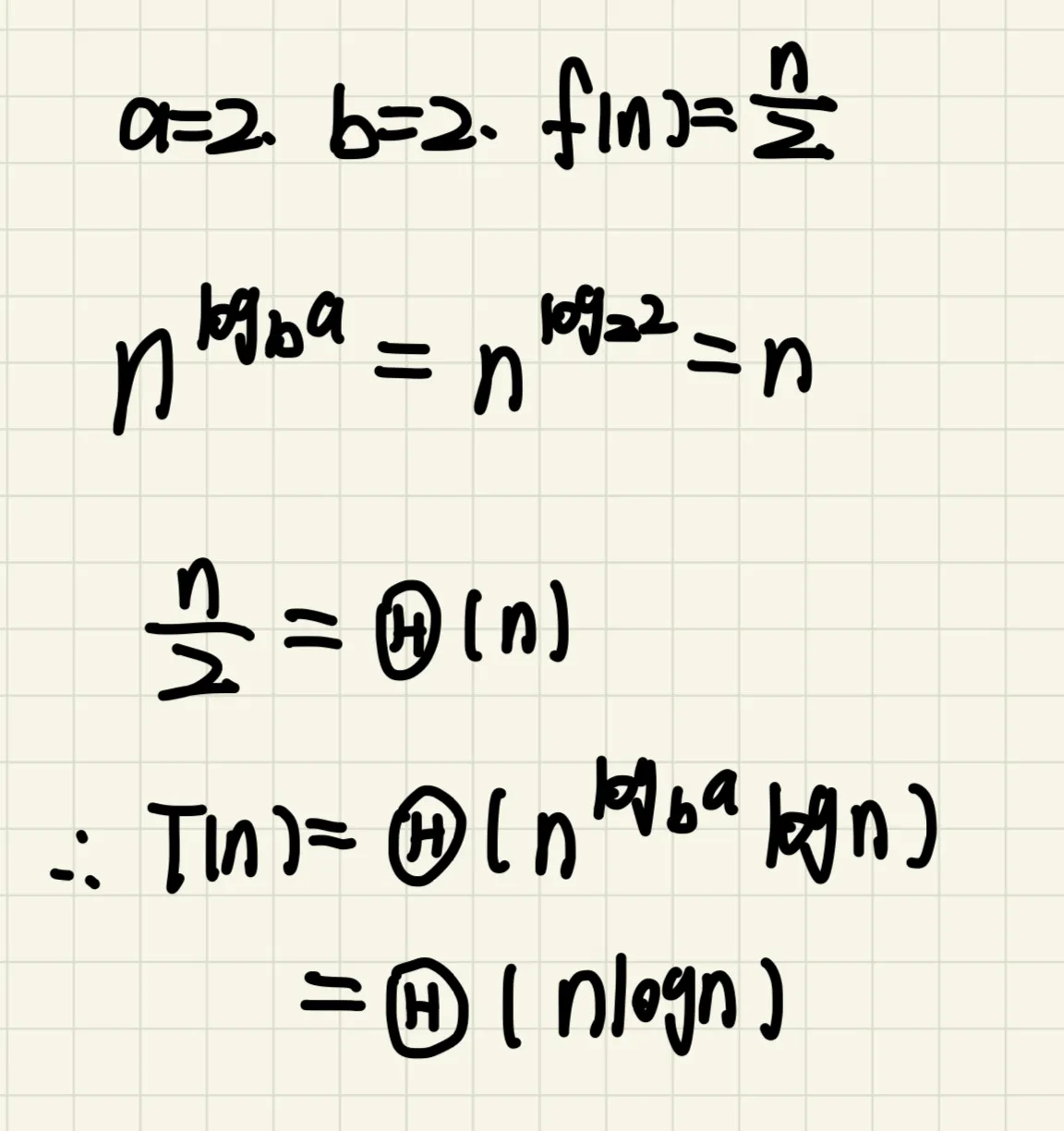
应用题
1、求解递推方程
T(n)=9T(n/3)+n

2、求解递推方程
T(n)=T(2n/3)+1

3、求解递推方程
T(n)=3T(n/4)+nlogn

4、求解递推方程
T(n)=2T(n/2)+nlogn
用到递归树求解。
在递归算法的时间复杂度分析中,递归成本通常是不可以忽略的,它对于确定总的时间复杂度至关重要。然而,有时在递归树的分析中,如果非递归部分的成本显著高于递归部分的成本,那么在总的时间复杂度中非递归成本会成为主导项。
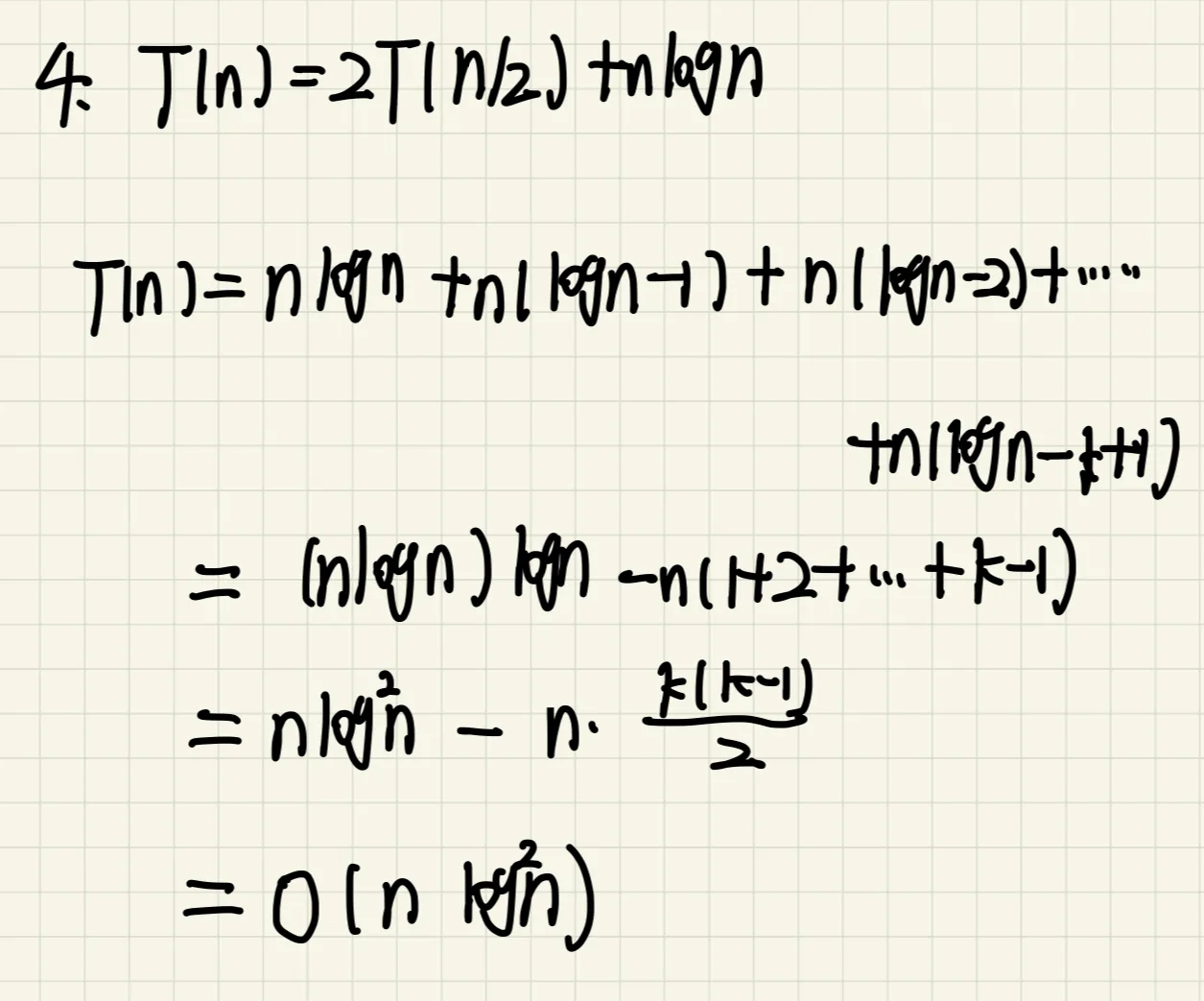


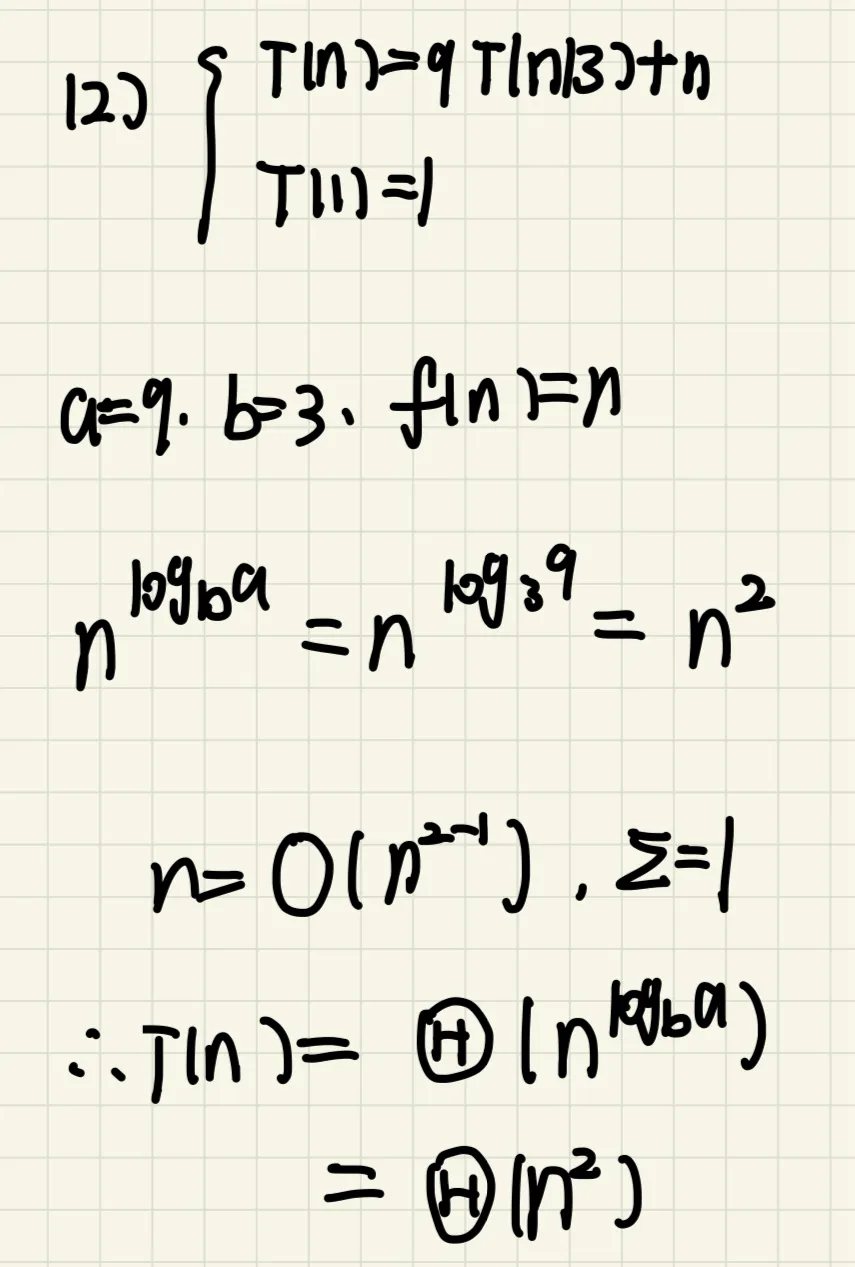


答案貌似有问题。


