期末复习题1
1、选择题
1.算法必须具备输入、输出和( )等 4 个特性。
A.可行性和安全性 B.确定性和易读性
C.有穷性和安全性 D.有穷性和确定性
答案:D
解析:
A选项提到的“可行性和安全性”,虽然重要,但并不是算法的基本特性。
B选项中的“易读性”,指的是代码的可读性和易于理解,这更多是编程实践的一个方面,而非算法本身的基本特性。
C选项同样提到了“安全性”,这并不属于算法的基本特性。
D选项提到了“有穷性和确定性”,这两个都是算法的基本特性。
2.算法分析中,记号 O 表示( B ),记号Ω表示( A )
A.渐进下界 B.渐进上界
C.非紧上界 D.紧渐进界
答案:B、A
解析:
大O记号(O) - 渐进上界:
定义: 大O记号用于描述算法的最坏情况运行时间的上限。当我们说一个算法的时间复杂度是O(f(n))时,
我们的意思是:在最坏的情况下,该算法的运行时间不会超过f(n)的某个常数倍。
例子: 如果一个算法的运行时间是O(n²),这意味着在最坏的情况下,它的运行时间增长率不会超过输入大小n的平方的某个倍数。
关键点: 这是一种对算法在最坏情况下性能的保守估计。
大Omega记号(Ω) - 渐进下界:
定义: 大Omega记号用于描述算法的最佳情况运行时间的下限。当我们说一个算法的时间复杂度是Ω(g(n))时,
我们的意思是:在最好的情况下,该算法的运行时间至少是g(n)的某个常数倍。
例子: 如果一个算法的运行时间是Ω(n),这意味着在最好的情况下,它的运行时间增长率至少与输入大小n的某个倍数相同。
关键点: 这是一种对算法在最佳情况下性能的乐观估计。
如果函数f(n)的渐近的上界和下界相等,都是g(n),则称g(n)是f(n)的渐近的紧的界。或称函数f(n)的阶是g(n)。
3.假设某算法在输入规模为 n 时的计算时间为 T(n)=3*2^n。在某台计算机上实现并
完成该算法的时间为 t 秒。现有另一台计算机,其运行速度为第一台的 64 倍,那
么在这台新机器上用同一算法在 t 秒内能解输入规模为多大的问题?( )
A.n+8 B.n+6
C.n+7 D.n+5
答案:B
解析:

4.设 问 题 规 模 为 N 时 , 某 递 归 算 法 的 时 间 复 杂 度 记 为 T(N) , 已 知 T(1)=1 ,
T(N)=2T(N/2)+N/2,用 O 表示的时间复杂度为( )。
A.O(logN) B.O(N)
C.O(NlogN) D.O(N²logN)
答案:C
解析:
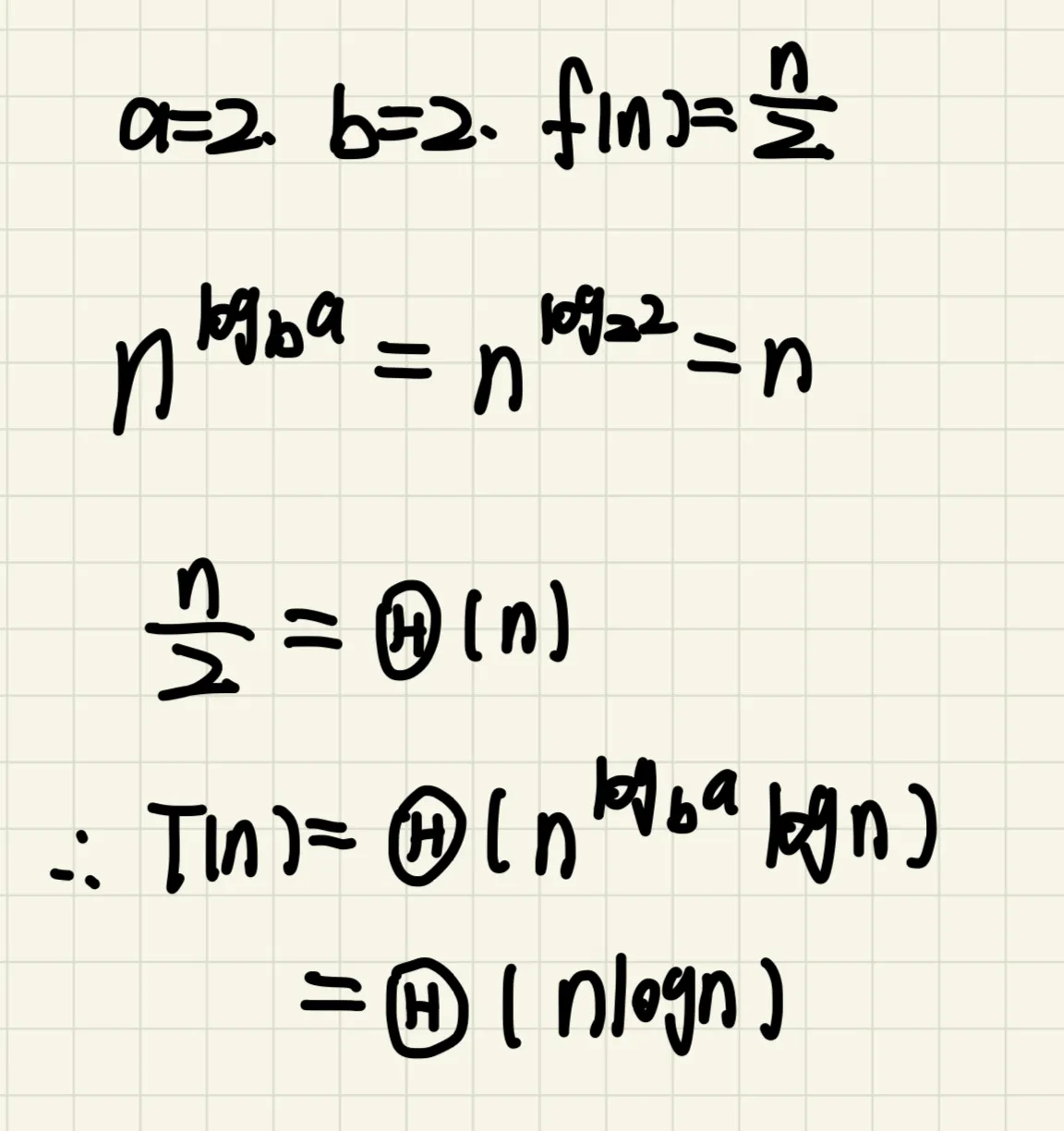
5.直接或间接调用自身的算法称为( B )。
A.贪心算法 B.递归算法
C.迭代算法 D.回溯法
答案:B
解析:
题目是关于一个特定类型的算法的定义:直接或间接调用自身的算法。这种算法的定义符合选项B - 递归算法。
递归算法(B):
定义: 递归算法是一种在其定义中直接或间接调用自身的算法。在递归算法中,问题被分解成更小的、类似的子问题,直到达到一个基本案例,
这个基本案例可以直接解决而不需要进一步递归。
例子: 一个典型的例子是计算斐波那契数列或阶乘。
其他选项:
A. 贪心算法:它是一种在每一步选择当前最好的解决方案的算法,不回头考虑之前的选择。这种方法并不包含直接或间接调用自身的特性。
C. 迭代算法:迭代算法通过重复执行一系列操作来解决问题,但这些操作不包括调用算法本身。
D. 回溯法:虽然回溯法经常使用递归来实现,但它是一种特定的算法,用于在解决问题的过程中穷举所有可能的解决方案,并“回溯”以找到最优解。
6.Fibonacci 数列中,第 4 个和第 11 个数分别是( )。
A.5,89 B.3,89
C.5,144 D.3,144
答案:B
解析:
1 1 2 3 5 8 13 21 34 55 89。
注:标准斐波那契数列的前两个数字是1和1。
8.一个问题可用动态规划算法或贪心算法求解的关键特征是问题的( )。
A.重叠子问题 B.最优子结构性质
C.贪心选择性质 D.定义最优解
答案:B
解析:
重叠子问题(A):
这是动态规划算法的一个关键特征。在动态规划中,问题被分解成子问题,这些子问题被多次解决。
动态规划通过存储这些子问题的解决方案来优化计算,避免重复工作。然而,这并非贪心算法的特征。
最优子结构性质(B):
这是动态规划和贪心算法共有的关键特征。如果一个问题具有最优子结构性质,那么问题的最优解
可以通过其子问题的最优解来构造。在动态规划中,我们利用这个性质来构建整体解决方案。
在贪心算法中,我们假设通过局部最优选择(每一步都做出当前看来最好的选择)可以达到全局最优解。
贪心选择性质(C):
这是贪心算法的特征,其中局部最优选择被假设为会导致全局最优解。然而,这并不是动态规划所特有的,
因为动态规划不依赖于单一的“贪心”选择;相反,它考虑了多种选择的可能性。
定义最优解(D):
定义最优解是解决任何优化问题的基本步骤,不特定于动态规划或贪心算法。
综上所述,最适合作为动态规划和贪心算法共有的关键特征的是最优子结构性质(B)。
这表明这两种算法都依赖于通过组合子问题的最优解来构造整体问题的最优解。因此,答案是 B. 最优子结构性质。
9.下列哪个问题不用贪心法求解( )。
A.哈夫曼编码问题 B.单源最短路径问题
C.最大团问题 D.最小生成树问题
答案:C
解析:
哈夫曼编码问题 (A): 这是一个经典的使用贪心策略的问题。在构建哈夫曼树时,总是选择频率最低的两个节点合并。
这是一个典型的贪心选择。
单源最短路径问题 (B): 特别是当我们考虑到Dijkstra算法时,这个问题可以通过贪心法解决。在每一步中,
算法都会选择当前最短的路径扩展到未访问的节点。
最大团问题 (C): 这个问题通常不使用贪心策略来解决。最大团问题是一个NP完全问题,意味着没有已知的多
项式时间算法(包括贪心算法)能解决所有情况。通常需要使用回溯、分支界限或者近似算法。书本P127,回溯和分支限界中提及。
最小生成树问题 (D): 这个问题可以通过贪心算法解决,如Kruskal算法或Prim算法。
这些算法在每一步都选择最小权重的边,以构建最小生成树。
10.下列算法中通常以自底向上的方式求解最优解的是( )。
A.备忘录法 B.动态规划法
C.贪心法 D.回溯法
答案:B
解析:
备忘录法 (A): 这通常与动态规划相关,但它更多地采用自顶向下的方法。在备忘录法中,原问题被分解成更小的子问题,
并且结果被存储(或“记忆化”),以避免重复计算。尽管它涉及到子问题的解决,但这种方法的执行顺序是从顶部问题开始,
逐渐深入到子问题。
动态规划法 (B): 动态规划是一种解决复杂问题的方法,通过将问题分解成更简单的子问题,并构建这些子问题的解决方案,
从而解决整个问题。动态规划可以采用自底向上或自顶向下的方法,但在经典的动态规划实践中,自底向上的方法更为常见。
在这种方法中,我们首先解决最小的子问题,并逐步构建更大的问题的解决方案。
贪心法 (C): 贪心算法在每一步都做出当下看起来最好的选择,以期望这会导致全局最优解。这种方法通常不是自底向上的;
相反,它从某个初始解出发,通过局部最优的选择来扩展这个解。
回溯法 (D): 回溯法是一种解决问题的算法,通过尝试分步的方法逐步找到问题的解决方法。当它遇到一个问题没有解决方
案的情况时,它会回退一步尝试其他可能的解决方案。这更像是一种自顶向下的探索方法,而不是自底向上。
综上所述,答案是 B. 动态规划法。动态规划法在求解最优解时,通常采用自底向上的方法,首先解决最小的子问题,
然后逐步向上构建,直到解决原始问题。
11.下列算法中不能解决 0/1 背包问题的是( )。
A.贪心法 B.动态规划
C.回溯法 D.分支限界法
答案:A
解析:
贪心法 (A): 贪心算法在每一步都做出在当前看来最优的选择。在 0/1 背包问题中,贪心算法可能会根据价值
或价值密度(价值除以重量)来选择物品。然而,这种方法不能保证总是得到最优解,因为它可能错过了更优的
组合,这些组合可能在初看时并不是最优的。因此,贪心法并不总是适用于解决 0/1 背包问题。
动态规划 (B): 动态规划是解决 0/1 背包问题的经典方法。它通过构建一个解决子问题的表格,并从最简单的
子问题开始,逐步解决更复杂的问题,最终找到最优解。
回溯法 (C): 回溯法是一种通过遍历所有可能情况来找到问题所有解的算法。对于 0/1 背包问题,回溯法可以
通过尝试包括或不包括每个物品来找到所有可能的组合,从而找到最优解。
分支限界法 (D): 分支限界法是一种用于解决优化问题和计数问题的方法,它系统地遍历候选解的树形结构。
在 0/1 背包问题中,它可以有效地剪枝,从而只搜索有希望的分支,也能找到最优解。
因此,答案是 A. 贪心法,因为它不能保证总是解决 0/1 背包问题。贪心法可能会提供一个解,但这个解不一定是最优的。
12.下列哪个问题可以用贪心算法求解( )。
A.LCS 问题 B.批处理作业问题
C.0-1 背包问题 D.哈夫曼编码问题
答案:D
解析:
LCS 问题 (A): LCS (最长公共子序列,Longest Common Subsequence)问题是寻找两个序列共有的最长子序列的问题。
这个问题不能用贪心算法有效解决,因为贪心选择可能导致错过更长的公共子序列。通常使用动态规划来解决。
批处理作业问题 (B): 这个问题通常指的是在计算机科学中的作业调度问题,需要考虑作业的顺序以优化总体性能。
这个问题的解决方案通常不是贪心的,因为局部最优选择可能不会导致全局最优。
0-1 背包问题 (C): 正如前面提到的,0-1 背包问题不能用贪心算法有效解决,因为贪心选择可能导致非最优解。
哈夫曼编码问题 (D): 这是一个通过构建最优前缀编码树来最小化编码总长度的问题。哈夫曼算法是一个贪心算法的经典例子,
它在每一步选择最低频率的两个节点合并,这种贪心选择可以保证找到最优的前缀编码。
因此,答案是 D. 哈夫曼编码问题。这个问题可以用贪心算法求解,因为在每一步合并频率最低的两个节点这一贪心策略可以
保证最终得到最优的前缀编码
13.用回溯法求解最优装载问题时,若待选物品为 m 种,则该问题的解空间树的结点
个数为( )。
A.m! B.2^(m+1)
C.2^(m+1)-1 D.2^m
答案:C
解析:
最优装载问题是一个典型的组合优化问题,可以通过回溯法来求解。在这个问题中,
我们需要决定哪些物品被装载以优化某个特定的目标(例如最大化价值或最小化重量)。
在用回溯法解决这类问题时,我们通常构建一个解空间树,其中每个节点代表一个决策
(装载或不装载某个物品)。对于 m 种待选物品,解空间树的每个层级代表对一个物
品的决策,每个物品有两种选择:装载或不装载。
A. m!: 这代表 m 种物品的所有排列,但在最优装载问题中,物品的排列顺序并不重要,重要的是哪些物品被选中。
因此,m! 不是解空间树节点数的正确表达。
B. 2^(m+1) 和 C. 2^(m+1)-1: 这两个选项都是基于二叉树的节点数计算的。在一个完全二叉树中,
如果树的高度为 h,那么它的节点总数是 2^h - 1(这是选项 C)。如果树的最后一层完全满了,那么节点总数
是 2^(h+1) - 1,这里 h = m,所以选项 C 是正确的。
D. 2^m: 这代表每个物品两种选择(装载或不装载)的所有可能组合。在一个有 m 个物品的问题中,
会有 2^m 种组合,但这只计算了树的叶子节点,没有包括决策树中的非叶子节点。
综上所述,答案是 C. 2^(m+1)-1。这是因为每个物品有两种选择(即二叉树),所以对于 m 种物品,
解空间树是一个高度为 m 的完全二叉树,其总节点数为 2^(m+1)-1。
14.二分搜索算法是利用( )实现的算法。
A.分治策略 B.动态规划法
C.贪心法 D.回溯法
答案:A
解析:
分治策略(A):在二分搜索中,我们将问题分解为更小的子问题。具体来说,我们将数组分为两部分,
并确定所寻找的元素是在左侧还是右侧。通过这种方式,我们每次都将搜索范围减少一半,直到找到
目标元素或者确定元素不存在。这是分治法的一个典型应用,因为我们在每一步都将问题划分为两个更小的部分。
动态规划法(B):与二分搜索不同,动态规划是解决具有重叠子问题和最优子结构的问题的方法。
它通常用于求解具有递推关系的问题,通过存储子问题的解来避免重复计算。二分搜索并不涉及重叠子问题或最优子结构的概念。
贪心法(C):贪心算法在每一步都采取当前看起来最优的选择,而不考虑整体的最优解。二分搜索不是
在每一步都寻找局部最优解,而是通过比较和切分来系统地缩小搜索范围。
回溯法(D):回溯算法是一种通过试错来寻找所有/某些解决方案的算法,当它通过尝试可能的分支找
到一个可能的解决方案时会回溯。二分搜索并不涉及试错或回溯;它是一种直接且系统的搜索方法。
因此,最适合描述二分搜索算法的是A. 分治策略。二分搜索通过不断地将问题分解为更小的部分,
并在每一步中减少搜索范围,直到找到答案或确定答案不存在。主人,这是二分搜索算法的基本解析。
15.下列不是动态规划算法基本步骤的是( )。
A.找出最优解的性质 B.构造最优解
C.算出最优解(应该是最优值) D.定义最优解
答案:A
解析:
要确定哪一个选项不是动态规划算法的基本步骤,我们需要回顾动态规划算法的关键特征和步骤:
定义子问题(D):在动态规划中,首先需要定义子问题。这是基本步骤之一,
因为动态规划算法依赖于解决重叠的子问题并使用这些解来构建整体问题的解。
计算子问题的最优解(C):这一步是动态规划中的核心。算法需要计算每个子问题的最优解,
并通常将这些解存储在一个表格中以避免重复计算。
构造最优解(B):一旦所有子问题的最优解都被找到,动态规划算法会从这些子问题的解中
构建出整个问题的最优解。这个步骤对于完成整个算法过程至关重要。
找出最优解的性质(A):这一步骤通常是指在解决问题之前理解问题的性质,例如最优子结构
和重叠子问题。虽然这对于设计一个有效的动态规划算法很重要,但它并不是动态规划算法本身的“步骤”,
而是解决问题之前的一个准备步骤。
综上所述,如果我们严格区分算法设计的准备工作和算法本身的执行步骤,那么可以认为“A. 找出最优解的性质”
并不直接属于动态规划算法的执行步骤,而是一个前期的准备或理论分析步骤。
因此,在这个上下文中,选项A可以被视为“不是动态规划算法基本步骤”的选项。
16.下面问题( )不能使用贪心法解决。
A.单源最短路径问题 B.N 皇后问题
C.最小花费生成树问题 D.哈夫曼编码问题
答案:B
解析:
在这个问题中,我们需要识别哪个问题不能使用贪心法解决。贪心算法是一种在每一步选择中都选取当前状态下最好的选择,
而不考虑以后可能产生的后果。这种方法对于某些问题来说是有效的,但对于其他问题则可能无法找到最优解。
让我们逐一分析这些选项:
单源最短路径问题(A):对于没有负权边的图,贪心算法是有效的。例如,Dijkstra算法就是一个使用
贪心策略来寻找单源最短路径的算法。
N皇后问题(B):这个问题要求在N×N的棋盘上放置N个皇后,使得它们互不攻击。这是一个典型的回溯
问题,因为你需要考虑所有皇后的放置方式来找到解决方案。贪心算法在这里不适用,因为在放置每个
皇后时,对当前棋盘最优的选择可能导致无法放置后续的皇后。
最小花费生成树问题(C):这个问题可以使用贪心算法解决。最著名的例子是Kruskal算法和Prim算法,
它们都是使用贪心策略来找到最小生成树的。
哈夫曼编码问题(D):这是一种压缩数据的方法,也是贪心算法的一个应用。在哈夫曼编码中,经常出现的
字符使用较短的编码,不常出现的字符使用较长的编码,这是一种典型的贪心选择方法。
综上所述,贪心法可以有效解决单源最短路径问题、最小花费生成树问题和哈夫曼编码问题。然而,对于N皇后
问题,贪心法由于其局限性(即在每一步都做局部最优选择)无法保证找到全局最优解。
因此,不能使用贪心法解决的问题是 B. N皇后问题。
17.用二分搜索算法在 n 个有序元素表中搜索一个特定元素,在最好情况和最坏情况
下搜索的时间复杂性分别为( )。
A.O(1),O(logn) B.O(n),O(logn)
C.O(1),O(nlogn) D.O(n),O(nlogn)
答案:A
解析:
二分搜索算法是一种在有序元素表中查找特定元素的高效方法。这个算法的核心思想是将搜索区间分成两半,
然后根据目标元素与中间元素的比较结果来确定接下来搜索的区间。现在,让我们来探讨这个算法在最好
情况和最坏情况下的时间复杂度。
最好情况:在最好的情况下,我们要找的元素恰好是中间元素,也就是说,在第一次尝试时我们就找到了目标。
在这种情况下,时间复杂度是 O(1),因为我们只进行了一次操作。
最坏情况:在最坏的情况下,每次比较都不会直接找到目标元素,我们需要不断地将搜索区间分成两半。
由于每次操作都将搜索区间减半,所以二分搜索的时间复杂度是 O(logn)。这意味着随着元素数量的增加,
所需的步骤数增加的速度是对数的。
所以,基于这些分析,我们可以看到选项 A(O(1),O(logn))是正确的答案。这个选项正确地描述了
二分搜索在最好情况下(即第一次就找到目标元素)和最坏情况下(即每次都需要将搜索区间分成两半
直到找到目标元素)的时间复杂度。
21.下列关于计算机算法的描述不正确的是( )。
A.算法是指解决问题的一种方法或一个过程
B.算法是若干指令的有穷序列
C. 算法必须要有输入和输出
D.算法是编程的思想
答案:C
解析:
A. 算法是指解决问题的一种方法或一个过程:这个描述是正确的。算法确实是一组定义清晰的指令集合,
用于解决特定的问题或执行特定的任务。
B. 算法是若干指令的有穷序列:这也是正确的。算法由一系列步骤组成,这些步骤有明确的开始和结束,
这意味着它们是有限的。
C. 算法必须要有输入和输出:这个描述是有争议的。大多数算法确实涉及输入和产生输出,但并非所有
算法都严格要求有输入。例如,某些算法可能只生成一系列数据(只有输出,没有输入),或者仅基于内
部状态执行操作(既无输入也无输出)。因此,这个描述可能被视为不完全正确。
D. 算法是编程的思想:这个说法是比较宽泛的。算法更准确地说,是解决问题的方法或步骤。它确实是编
程中一个重要的组成部分,但将算法仅描述为“编程的思想”可能过于简化了其定义和重要性。
根据上述分析,最可能被认为不正确的描述是 C. 算法必须要有输入和输出。虽然大多数算法确实涉及
输入和输出,但这并非算法的绝对要求。因此,C 选项是这个问题的答案。
24.分治法所能解决的问题应具有的关键特征是()
A.该问题的规模缩小到一定的程度就可以容易地解决
B.该问题可以分解为若干个规模较小的相同问题
C.利用该问题分解出的子问题的解可以合并为该问题的解
D.该问题所分解出的各个子问题是相互独立的
答案:C
解析:
分治法是一种重要的算法设计策略,主要用于解决复杂问题。这种方法的核心是将大问题分解成若干个小问题,
单独解决这些小问题,然后将解决方案合并以解决原来的大问题。我们来逐一分析给出的选项:
A. 该问题的规模缩小到一定的程度就可以容易地解决:这个描述是分治法的一个特征,但它不是分治法的关键特征。
小规模问题更容易解决是许多算法共有的特性,并非分治法特有。
B. 该问题可以分解为若干个规模较小的相同问题:这是分治法的一个重要特征。将大问题分解为多个小问题是分治
法的核心步骤之一。
C. 利用该问题分解出的子问题的解可以合并为该问题的解:这是分治法的关键特征。分治法的核心不仅在于分解问题,
还在于能够将子问题的解有效地合并成原问题的解。
D. 该问题所分解出的各个子问题是相互独立的:这也是分治法的一个重要特征,因为它使得子问题可以独立解决,
甚至可以并行处理。
虽然所有这些选项都描述了分治法的某些特征,但关键在于如何将子问题的解合并成原问题的解。因此,选项 C
是最准确的答案。在分治法中,能否将子问题的解有效组合成原问题的解是整个策略成功与否的关键。