0、考察重点
题4,第五章回溯
关键词
1、解空间,构造是关键
2、两个基本的类型(a.子集树 b.排列树)
注:
1、画出树,解结构的形态
2、求解最优,并解释表达的内涵
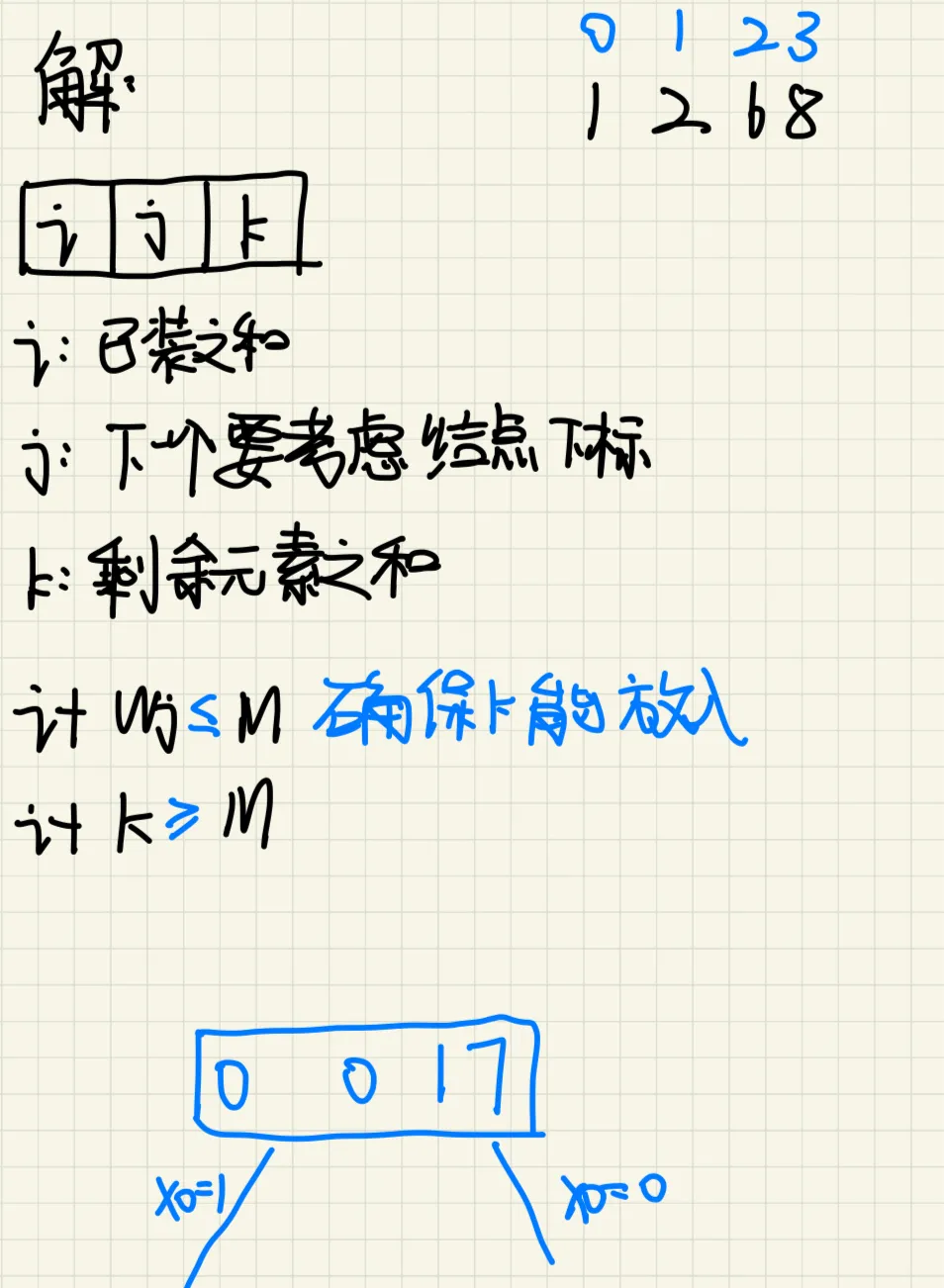
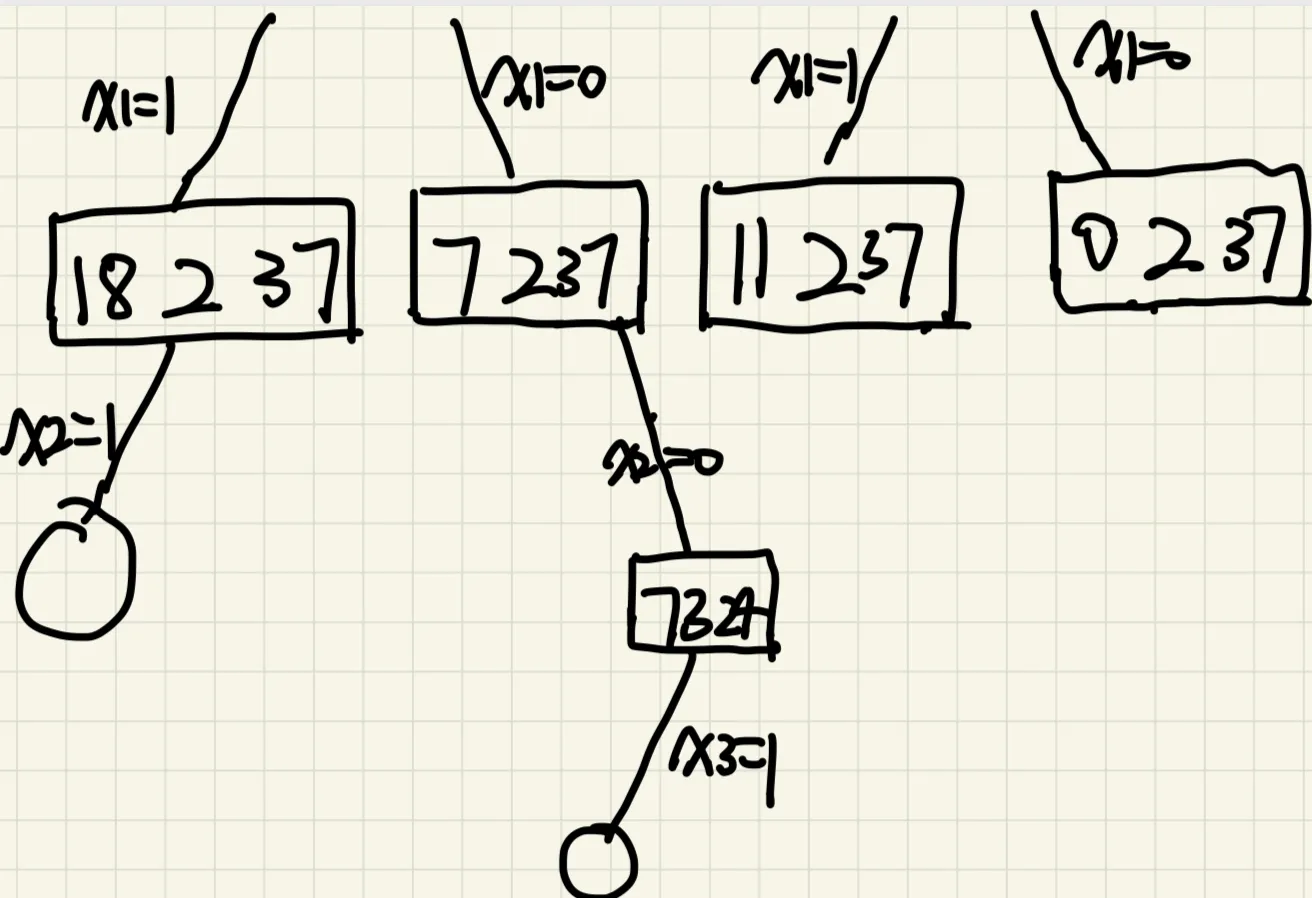
1、求解子集和数的问题:设有n=4个正数的集合S={1,2,6,8}和整数M=9,
请画出回溯法求解过程中产生的状态空间树,并给出所有子集和为M的可行解(x0,x1,x2,x3)。
解答:
状态空间树:
所有子集和为M的可行解
(1,1,1,0)
(1,0,0,1)
这种表达方式(1, 1, 1, 0)和(1, 0, 0, 1)是在说,
每个数字代表一个决策:1 表示包括该元素,0 表示不包括。
因此,(1, 1, 1, 0) 表示包括 {1, 2, 6} 这三个元素,而 (1, 0, 0, 1) 表示包括 {1, 8} 这两个元素。
所以,正确的答案是:
所有子集和为 M 的可行解为 (1, 1, 1, 0) 和 (1, 0, 0, 1),分别对应于子集 {1, 2, 6} 和 {1, 8}。
2、请画出用回溯法解4皇后问题的解空间树和搜索空间树:
解答:
略。
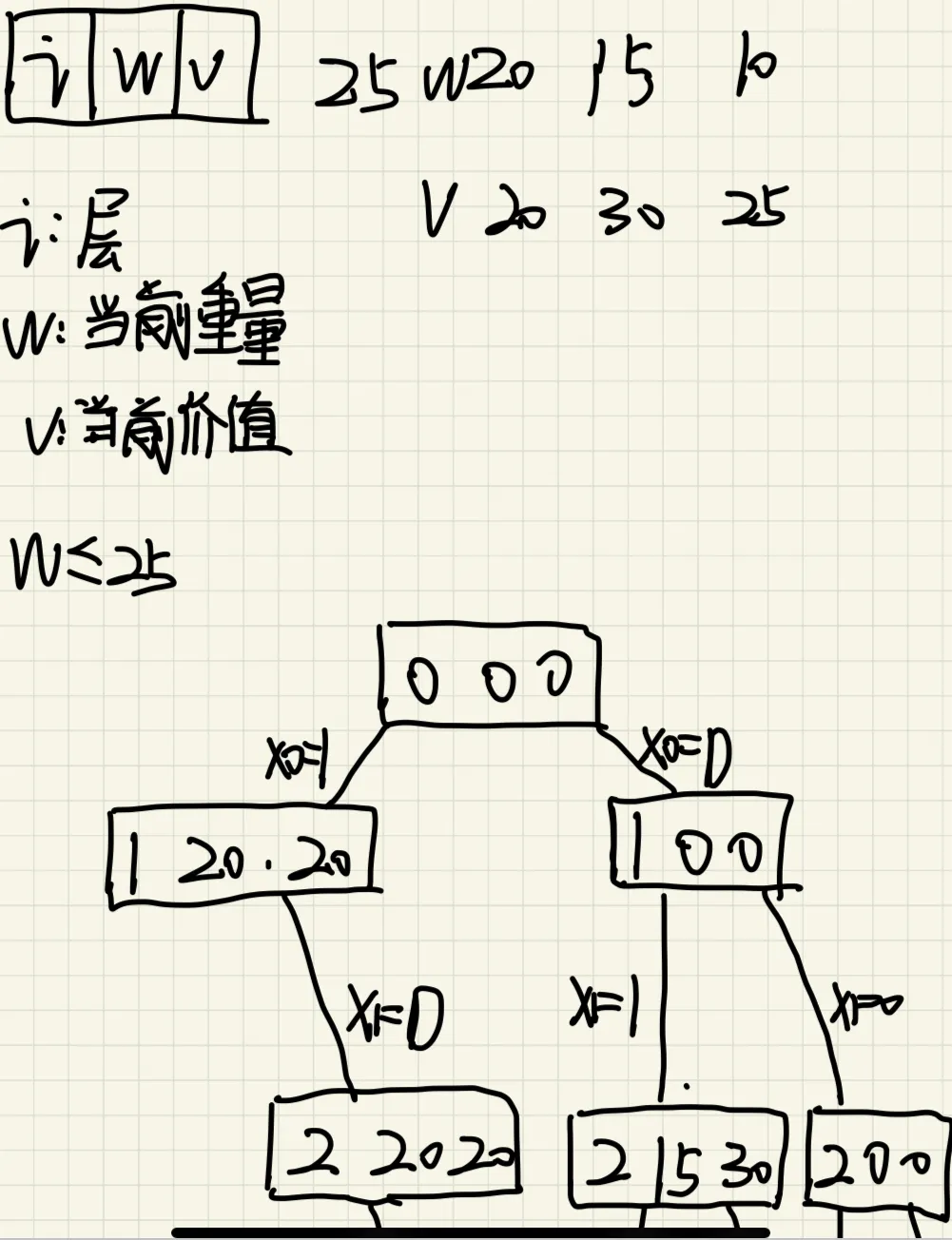
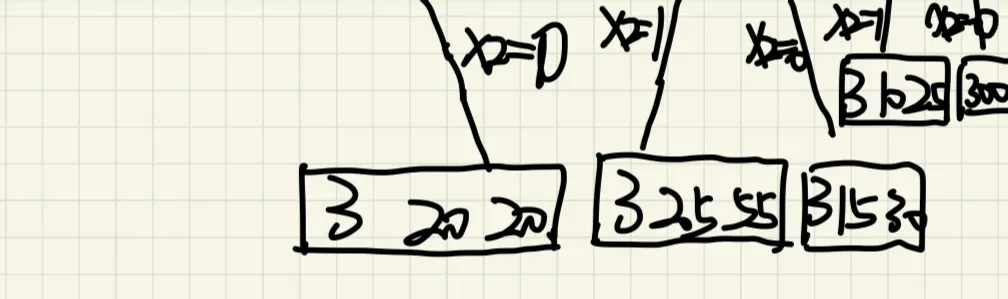
3、请画出用回溯法解n=3的0-1背包问题的解空间树和当三个物品的重量为{20, 15, 10},
价值为{20, 30, 25},背包容量为25时搜索空间树。
解空间树如下图:
最优解为:
(0,1,1)
最优值为55
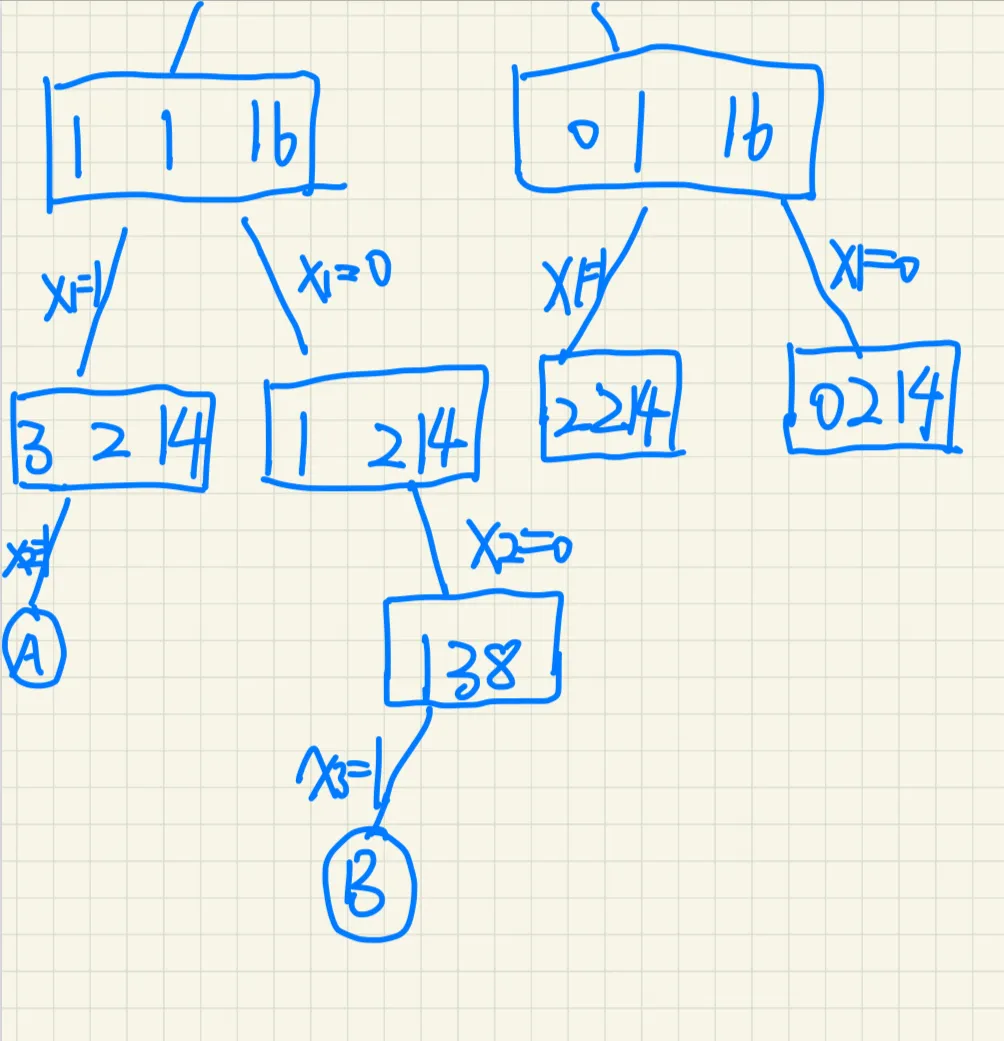
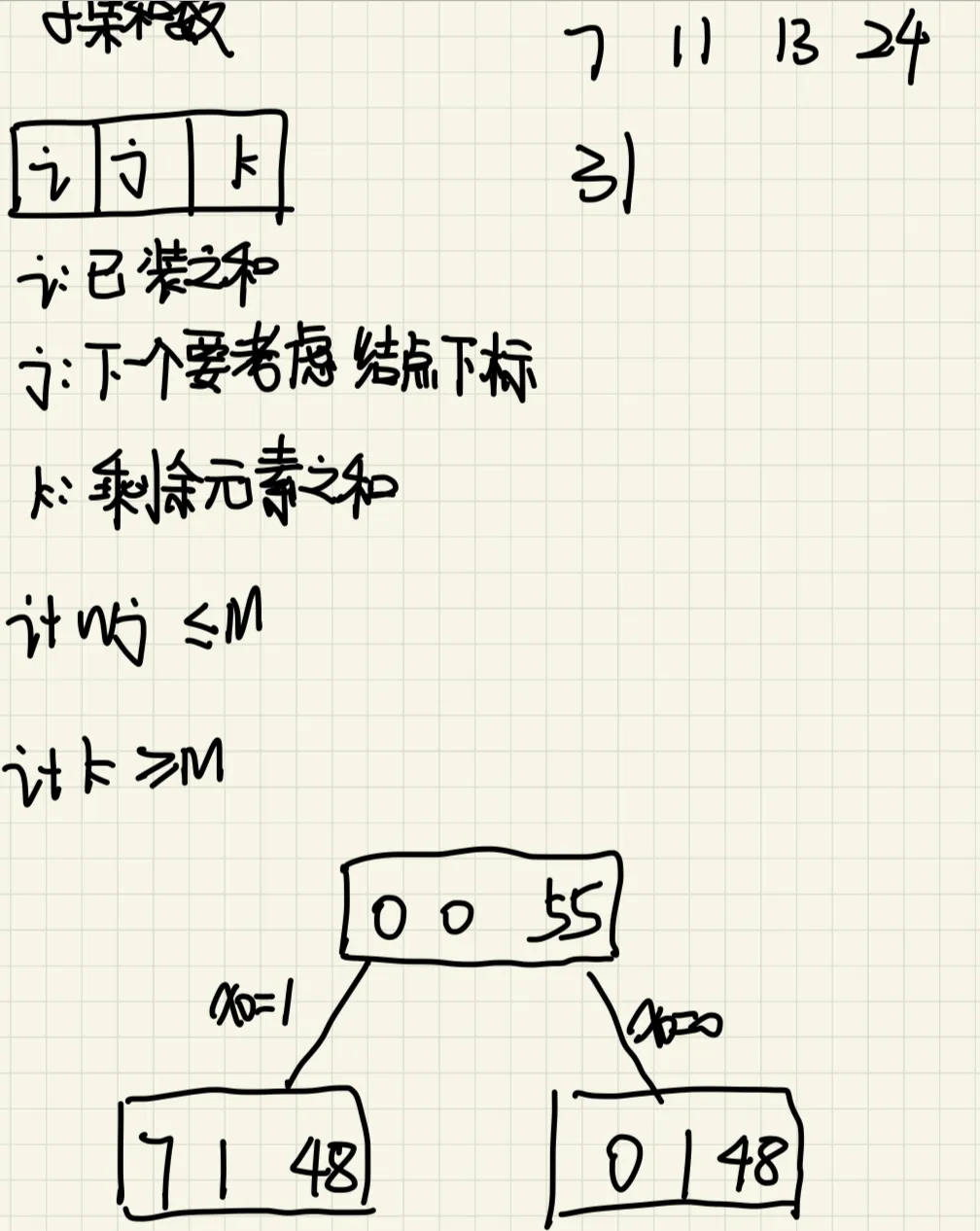
4、子集和数的问题:设有n=4个正数的集合W={w0,w1,w2,w3}={7,11,13,24}和正数M=31,
求W的所有满足条件的子集,使子集中的正数之和等于M。
请画出由SumOfSub算法实际生成的那部分状态空间树,并给出所有可行解。(采用固定长度4-元组表示解)
解答:
状态空间树如下图所示:
可行解:
(1,1,1,0)
(1,0,0,1)
5、0-1背包问题
假设你有一个背包,最大承重为W,以及一系列物品,每个物品都有自己的重量和价值。
目标是选择一些物品放入背包中,使得所选物品的总价值最大,同时不超过背包的承重限制。
物品的重量和收益分别是:
• 重量: w = [10,15,6,9]
• 收益:v =[2,5,8,1]
• 背包的最大载重:M = 32
任务:
1. 解空间的构造:
描述0-1背包问题的解空间如何构造。解释这个解空间的结构是如何与子集树相关的。
2. 绘制解空间树:
给定一个简单的物品列表,画出对应的子集树。标注出每个节点的决策(是否选择该物品)。
3. 求解最优解:
通过回溯算法在你绘制的树上求解最优解。解释在此过程中如何剪枝优化搜索。
4. 最优解的内涵解释:
解释在0-1背包问题中最优解的含义。
1.解空间的构造
0-1背包问题的解空间可以构造为一个子集树。在这个树中,每个节点代表一个决策-是否将特定的物品放入背包中。
每层代表一个物品。
每个节点有两个分支:一个代表选择当前物品(将其放入背包),另一个代表不选择(不将其放入背包)。
解空间的每个路径(从根到叶的路径)代表一个可能的物品组合。
0-1背包问题的解空间结构与子集树紧密相关,因为这个问题本质上是在寻找一个物品的子集,
该子集的总重量不超过背包的最大承重,同时总价值最大化。这里的关键在于选择物品的组合,这正是子集树所表示的。
2.解空间树的绘制:
左分支表示选择该物品,右分支表示不选择该物品。
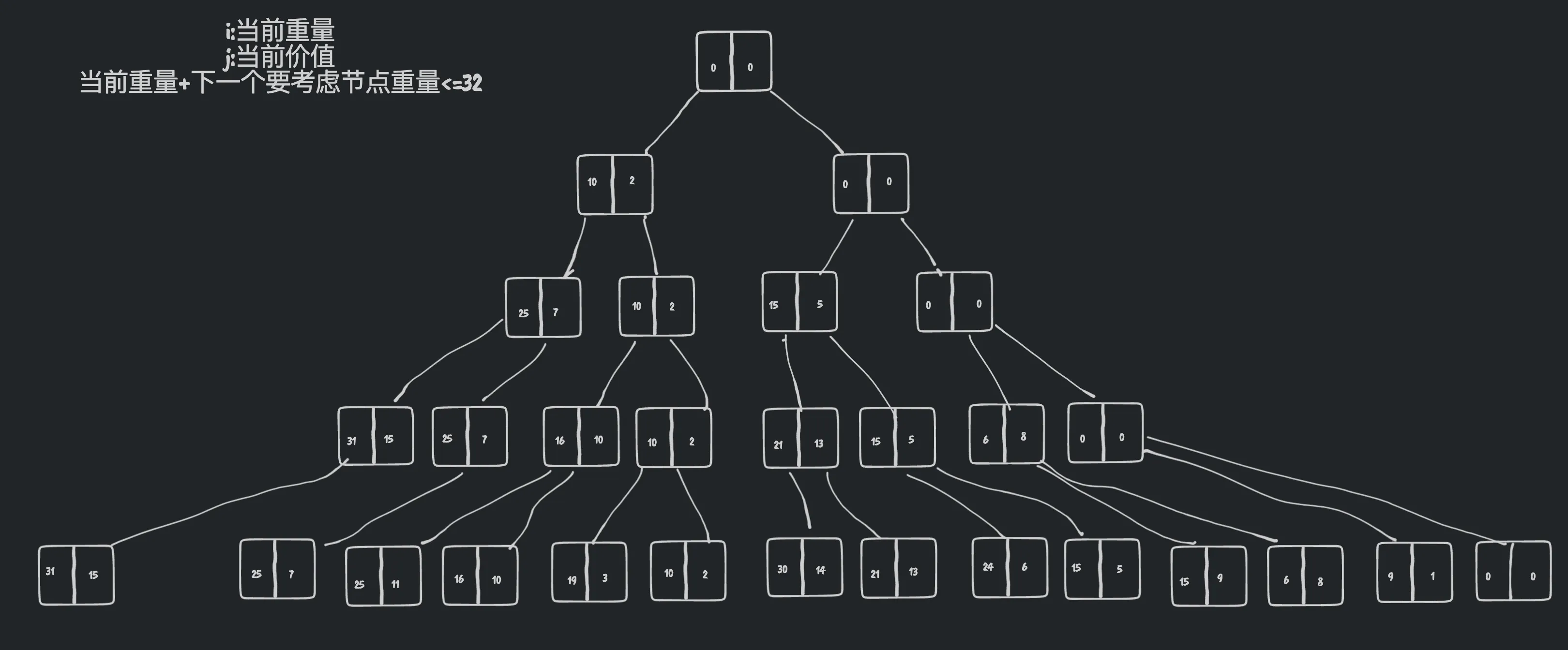
3.求解最优解:
在绘制的树上使用回溯算法时,您可以通过检查当前的总重量是否超过
背包的最大载重来剪枝。如果超过,则终止当前分支的搜索。此
外,您还可以通过比较当前的总价值与已知最优解的价值来剪枝。
如果当前分支即使加上所有剩余物品的价值也无法超过已知的最优解,则该分支不会产生更好的结果,可以被剪掉。
4. 最优解的内涵解释:
在0-1背包问题中,“最优解”是指在不超过背包承重限制的条件下,可以获得的最大总价值的物品组合。
这通常涉及在物品的重量和价值之间进行权衡,找到最佳组合以最大化价值。
您的解决方案选择了前三个物品,即w =[10,15,6]和v=[2,5,8],
总重量是10+15+6=31,总价值是2+5+8=15。这个总重量没有超过背包的最大载重M=32,
并且在不违反此限制的情况下,您已经找到了最大的总价值,所以这确实是最优解。
6、旅行商问题(TSP)
假设有一组城市和每对城市之间的旅行成本,目标是找到一条最短的路径,
访问每个城市恰好一次,并最终返回出发城市。
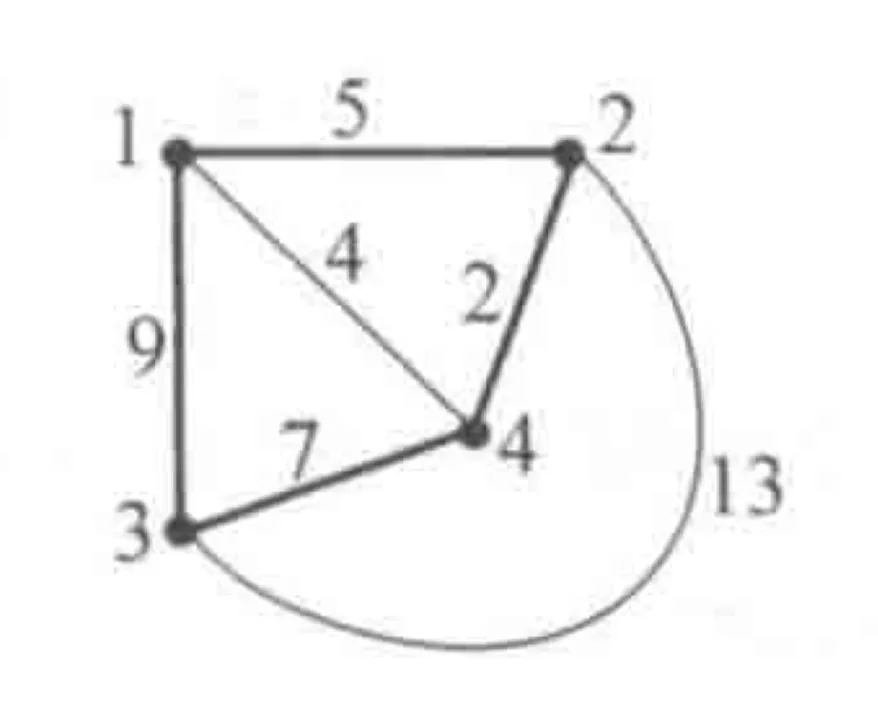
城市集合和路径成本信息如下:
城市集合:{1,2,3,4}
成本:
• 1到2的成本是5
• 1到3的成本是9
• 1到4的成本是4
• 2到3的成本是13
• 2到4的成本是2
• 3到4的成本是7
任务:
1. 解空间的构造:
描述TSP问题的解空间如何构造。解释这个解空间的结构是如何与排列树相关的。
2. 绘制解空间树:
画出对应的排列树。标注出每个节点的决策(选择下一个访问的城市)。
3. 求解最优解:
通过回溯算法在你绘制的树上求解最优解。解释在此过程中如何剪枝优化搜索。
4. 最优解的内涵解释:
解释在TSP问题中最优解的含义。
解答:
1.解空间的构造
TSP问题的解空间是通过城市的所有可能排列来构建的。这个解空间的结构是与排列树相关的,
排列树是一个有序树,通常用来表示对象的所有可能排列。
•树的节点:代表一个部分解,即到目前为止的路径。
•树的边:代表从一个城市到另一个城市的决策。
•叶节点:代表完成的路径,即访问了所有城市一次并返回出发城市的路径。
2.解空间树
假设有4个城市,我们可以用排列树来表示所有可能的路径。以下是一个简化的排列树示例:
(1)
/ | \
/ | \
(2) (3) (4)
/ \ / \ / \
(3) (4)(2) (4)(2) (3)
| | | | | |
(4) (3) (4) (2) (3) (2)
在这棵树中,我们从城市1开始,然后选择下一个要访问的城市,直到访问了所有的城市。
3.求解最优解
使用回溯算法求解最优解时,我们可以通过当前路径的总成本以及剩余城市的最小可能成本来剪枝。
•成本剪枝:如果当前路径的总成本已经超过了已知的最低成本路径,那么这个分支就不会产生最优解,可以被剪掉。
•界限函数:可以用来估计完成当前路径所需的最小成本,如果该成本大于已知的最低成本,则当前路径不再考虑。
以下排列成本为:
• 1-2-3-4-1:29
• 1-2-4-3-1:23
• 1-3-2-4-1:28
• 1-3-4-2-1:23
• 1-4-2-3-1:28
• 1-4-3-2-1:29
最优解的路径是1-2-4-3-1,总成本为23。这条路径访问了每个城市一次,并且总旅行成本是最低的。
4. 最优解的内涵解释
在TSP问题中,最优解是指访问每个城市恰好一次,并返回出发城市的路径中,总旅行成本最低的路径。
这意味着,如果我们有多条可能的路径,最优解是这些路径中总成本最低的那一条。
7、装载问题
有一艘船和一系列货物,假设船容量为8,货物有3个,重量分别为5,3,1。
要求重量最大,不能超重。
任务:
1.解空间的构造:
描述装载问题的解空间如何构造。解释这个解空间的结构是如何与子集树相关的。
2.绘制解空间树:
画出对应的子集树。标注出每个节点的决策(选择将该货物装载到哪艘船上)。
3.求解最优解:
通过回溯算法在你绘制的树上求解最优解。解释在此过程中如何剪枝优化搜索。
4.最优解的内涵解释:
解释在装载问题中最优解的含义。
解答:
1.解空间的构造
装载问题的解空间可以通过构建一个子集树来表示,其中每个节点代表一个装载决策阶段。
这个解空间的结构与子集树相关,因为我们在每个阶段都在做选择一要么将货物装入船中,要么不装。
•树的节点:代表一个部分解决方案,即在某一阶段货物的装载状态。
•树的边:表示是否选择将当前考虑的货物装入船中。左分支可以代表选择装载当前货物,右分支代表不装载。
•树的深度:等于货物的数量,每个层级代表对一个新货物的装载决策。
2.绘制解空间树
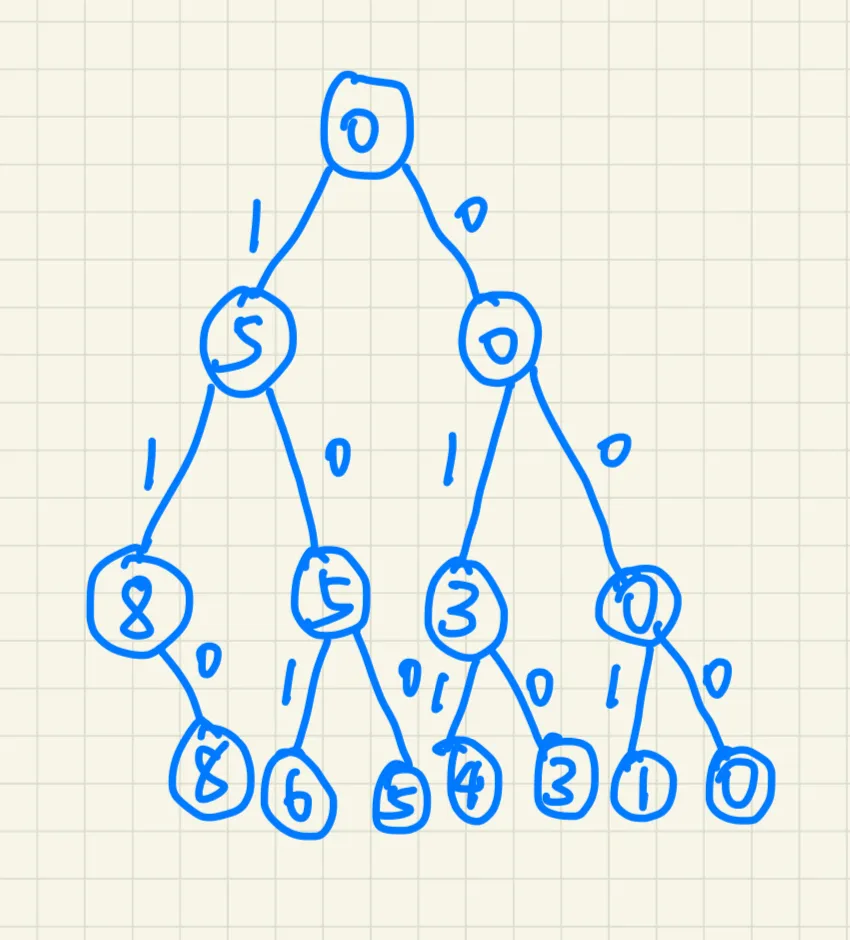
每个分支代表一个货物的装载决策,例如,左边的分支代表装载当前货物,右边的分支代表不装载。
3.求解最优解
通过回溯算法在树上求解最优解时,我们会跟踪当前的装载量,并确保它不超过船的最大载重量。
我们可以通过以下方式进行剪枝:
•如果任何决策导致当前装载量超过最大载重量,那么这个决策路径会被剪掉。
•如果当前的决策路径已经达到或超过了最大可能装载量,那么无需进一步探索该路径。
4.最优解的内涵解释
在装载问题中,最优解是指在不超过船的最大载重量的前提下,可以装载的最大货物重量。
这通常意味着尽量装满船的容量,而不是平衡不同船只的装载量,因为这里只有一艘船。
对于给定的例子,我们的目标是装载尽可能多的货物,直到达到船的最大载重量为止。
在这个特定的例子中,我们可以将重量为5和3的货物装入船中,总重量为8,
这是在不超重的条件下的最优解是将重量为5和3的货物装入船中,总装载重量为8。








